Porting ISAAC to Python

3 months ago, I discovered an algorithm called ISAAC on reddit. ISAAC (Indirection, Shift, Accumulate, Add, and Count) is a cryptographically secure pseudorandom number generator (CSPRNG) designed in 1996 by Bob Jenkins. It produces 32-bit unsigned integers uniformly distributed, unbiased, and unpredictable. Cycles are guaranteed to be a minimum of 2⁴⁰ values long and they are 2⁸²⁹⁵ values long on average. The generator runs fast and performs 18.75 machine cycles on average .

I’ve wanted to write my first Python extension for a long time; the short C implementation combined with a simple API solely composed of two functions – one for initializing the generator, one for generating random numbers – made ISAAC a great candidate for this task.

Writing Python extensions is easy

Given my inexperience, this post is not going to be an umpteenth tutorial about writing extensions, I would rather link you toward resources I found useful for this purpose. However, I would like to point out how easy it is to write extensions: Python’s documentation is clear, extensive, and provides a great example that guides you step by step. In addition, the C API is simple and well documented too. This makes writing extensions a very pleasant experience.

Here’s what you need to get started:

• Extending and Embedding the Python Interpreter, Python’s official documentation;
• Python Extension Programming with C, Tutorials Point;
• Python modules in C, Dan Foreman-Mackey.

The rest depends on your C skills. Hello, segmentation fault!

Code

Since, I’m a very fancy guy, I named the package… drum roll… “pyisaac”! The code is available on GitHub under MIT license. I’m far from being a C expert, comments, and PR are very welcome. The package is hosted on PyPI and can be installed via pip or easy_install:

$ pip install pyisaac
$ easy_install pyisaac

Use

As for the original implementation, the API is simple:

>>> import pyisaac
>>> pyisaac.random()
0.3417196273803711
>>> pyisaac.seed('pyisaac')
>>> pyisaac.random()
0.9284197092056274

Implementation

seeding routine

Bob Jenkins provides no official seeding routine for the algorithm. At first, as suggested by redditor BonzaiThePenguin, I used 1024 bytes of data from /dev/random. Since this source of randomness is potentially blocking (more about it here and there) and not cross-platform, later, I’ve decided later to rely on Python os.urandom(). On a UNIX-like system this function will query /dev/urandom and on Windows it will use CryptGenRandom(). If no randomness source is found, the algorithm is seeded from the system time and then MUST NOT be used for cryptographic purposes.

when unsigned long integers were short

I have slightly modified the original file standard.h. ISAAC relies on 4-byte integers arithmetic. Back in 1996, unsigned long integers were 4-byte long but nowadays, they are an 8-byte quantity on 64-bit processors. So I replaced them with unsigned integers instead.

mapping integers to floats in [0, 1]

ISAAC generates random integers ranging from 0 to 2³²-1. In theory dividing them by 2³²-1 should produce distinct floating point numbers between 0 and 1. In practice, this doesn’t work very well, as illustrated by the following C code snippet:

#include <stdio.h>

int main(int argc, char** argv) {
    float a, b, c, ONE = 1.0;
    unsigned int MAXUINT = 0xFFFFFFFF;

    a = 0xFFFFFF01 / (float)MAXUINT;
    b = 0xFFFFFF02 / (float)MAXUINT;
    printf("%d\n", a == b);

    c = 0xFFFFFF80 / (float)MAXUINT;
    printf("%d\n", ONE == c);
}

Output:

1
1

This behavior is related to how floating point numbers are represented. The precision offered by the float type is not enough to account for the infinitesimal increment between a and b and causes collisions.

double to the rescue

To circumvent this problem, pyisaac relies on the double type. A double is 64-bit long whereas a float is 32-bit and is sufficiently accurate to map each integer to a distinct floating point number between 0 and 1.

one and one makes two

This approach presents a drawback: the generated doubles have a 32-bit resolution and do not make the most of the extra precision brought by the double type. I’ve taken a look at how CPython random generator is implemented and the core developers came out with an elegant solution: two 32-bit random numbers are generated in order to “fill” one double and achieve 53-bit resolution:

/* generates a random number on [0,1) with 53-bit resolution; note that
 * 9007199254740992 == 2**53; I assume they're spelling "/2**53" as
 * multiply-by-reciprocal in the (likely vain) hope that the compiler will
 * optimize the division away at compile-time.  67108864 is 2**26.  In
 * effect, a contains 27 random bits shifted left 26, and b fills in the
 * lower 26 bits of the 53-bit numerator.
 */
static PyObject *
random_random(RandomObject *self)
{
    unsigned long a = genrand_int32(self) >> 5, b = genrand_int32(self) >> 6;
    return PyFloat_FromDouble((a * 67108864.0 + b) * (1.0 / 9007199254740992.0));

Neat, isn’t it?

Testing

testing the implementation

Bob Jenkins provides a seed and the first 2600 random numbers generated from it. pyisaac is tested against these numbers and gets them right… but this only means the implementation is right, not that the algorithm generates truly uniformly distributed, unbiased, and unpredictable numbers.

testing the algorithm

In fact, it is impossible to mathematically demonstrate that a generator is indeed a random bit generator. Consequently, generators are submitted to batteries of statistical tests which aim to detect certain kinds of weaknesses such as:

• shorter than expected periods for some seed states;
• lack of uniformity of distribution for large amounts of generated numbers;
• correlation of successive values, etc.

Dieharder is an example of such a battery of tests. ISAAC successfully passes all the Diehard and NIST statistical tests. Both these test suites are part of Dieharder.

Performance

Let’s get a rough sense of how pyisaac performs compared to random.random() from the standard library and numpy.random.rand(). These PRNGs implement the Mersenne twister algorithm:

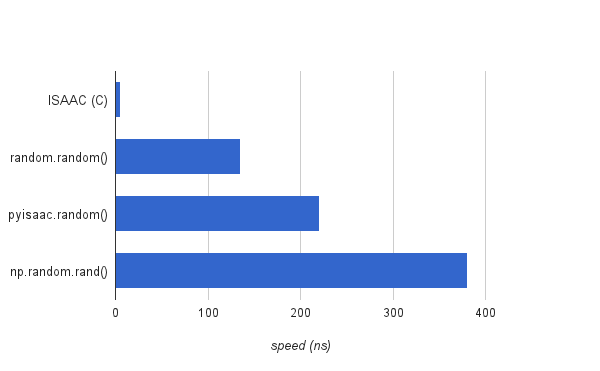
As can be seen, pyisaac runs within the same order of magnitude. And… yes… Python adds much overhead compared to the native implementation… But starting a flame war is not the point of this post :)

That’s all folks! I’d like to thank Mike McFadden who gave me valuable advice on how to seed the generator properly.